Foundations of Intelligent Learning Agents

The assignments/projects for the course can be found here.
Refer the course website for more information.

Regret Minimization Algorithms for Multi Armed Bandit Formulations

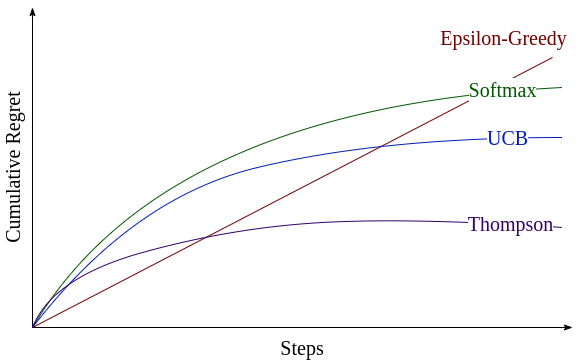
Multi Armed Bandit

Multi Armed Bandit Problems require regret minimization algorithms to optimize the explore-exploit tradeoff for different horizon scales.
In the first assignment, I implemented the Epsilon-Greedy algorithms for linear regret.

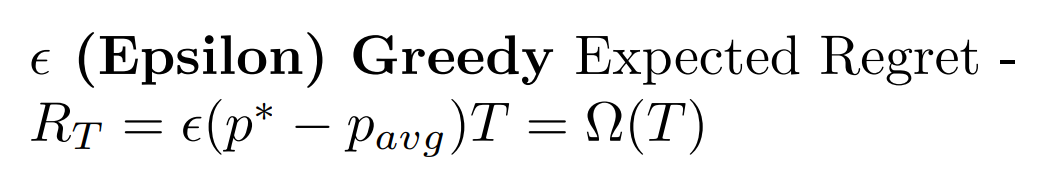
epsilon greedy

Later on, I used UCB, KL-UCB and Thompson Sampling algorithms which are in accordance with the Lai-Robbins logarithmic bound.

ucb, klucb

Later on, the problem of having finite stage feedback was encountered, where we get to know about the regrets only after a batch of samples, and we need to provide the distribution of which arms to be pulled and how frequently in the next batch. Thompson Subsampling was implemented for finite-stage feedback formulation.

The next task was to find an algorithm that works well when the number of arms is comparable to the horizon T. GLIE-ified Epsilon Greedy with quantile regret minimization was implemented for num_arms A = horizon T. (GLIE - Greedy in the Limit, Infinite Exploration)

Assignment repository can be found here.
Assignment report can be found here.

Policy Evaluation, Improvement and MDP Planning

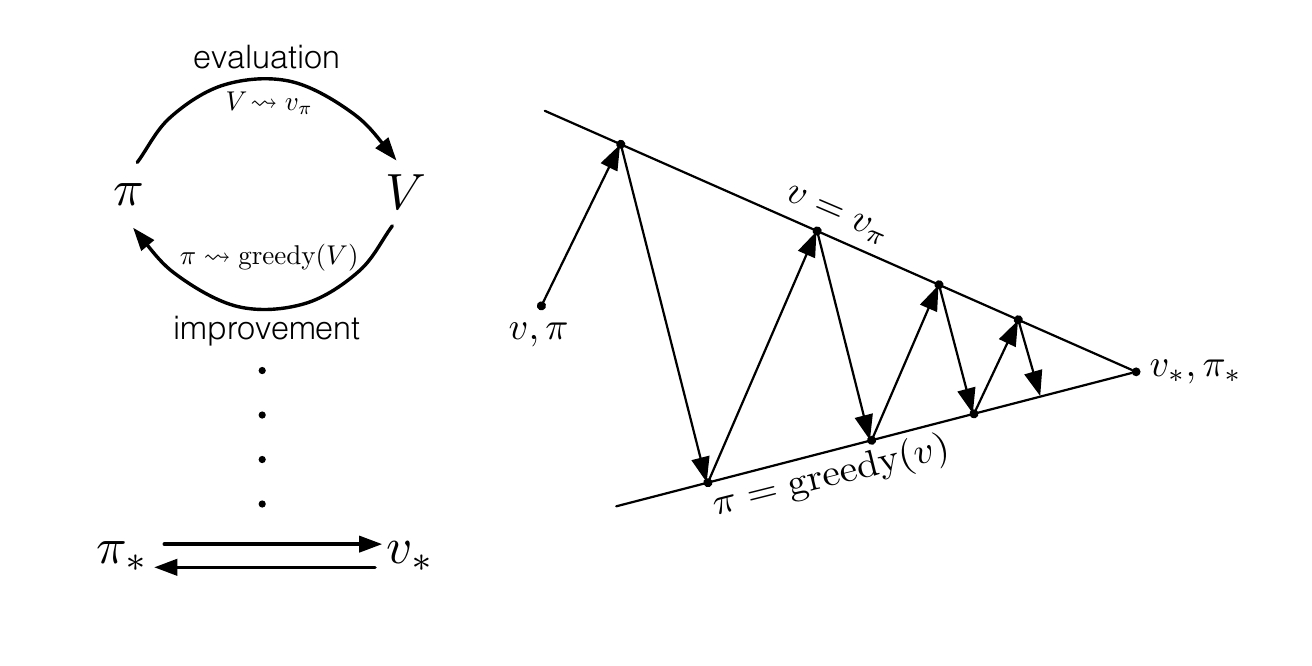
Policy Iteration

Given any Markov Decision Process (MDP), we need to determine the Optimal Value Function V* and Optimal Policy π*. I implemented three different algorithms for this purpose -

  • Value Iteration - It iteratively updates the value function of each state in the MDP, leading to guaranteed convergence in countably finite number of iterations value iteration

  • Howard’s Policy Iteration - HPI is a policy improvement algorithm, which randomly chooses improvable states, and creates new policies based on the Action Value Function of the MDP. This is also guaranteed to converge, by the Banach’s Fixed Point theorem.
  • Linear Programming - We create a set of n*k linear inequalities from the n Bellman Equations, and use an off-the-shelf linear solver to get the otimal value function of the MDP.

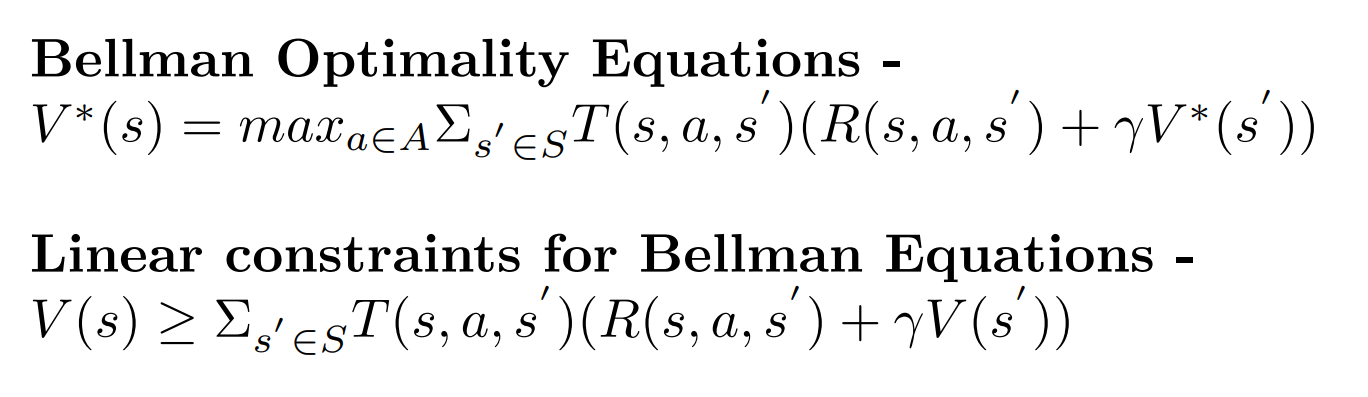
Bellman Equations

Assignment repository can be found here.
Assignment report can be found here.